Une course contre le temps

1. I.Introduction
   

Les processeurs de traitement du signal, ou DSP en anglais pour Digital Signal Processor, ont fait leur apparition dans le domaine industriel et audionumérique professionnel depuis les années 80 (pour les premiers). Leur utilisation pour un usage domestique n’est vraiment survenue que vers le milieu des années 90.

Bien que son nom sous-entende un système numérique complet, cette technologie et les composants l’entourant couvrent un panel de disciplines plutôt vaste :

1. •électronique analogique
   

2. •électronique numérique
   

3. •microprocesseur
   

4. •informatique
   

5. •mathématiques du signal
   

Ce qui va nous intéresser ici est principalement le microprocesseur DSP. Il faut savoir que les domaines d’utilisation du traitement du signal sont très variés, allant de la simple restitution sonore aux automatismes, en passant par la synthèse ou la reconnaissance vocale, la compression de données (MP3, JPEG, etc…), l’analyse de signaux (FFT…), télécommunications,… A chaque domaine va correspondre un DSP, ainsi sa puissance et son coût de développement seront des critères de sélection très importants.

Nous verrons au travers de ce document ce qui va influencer la puissance d’un DSP et donc comprendre pourquoi un processeur normal ne fait pas aussi bien.

2. II.Généralités du numérique
   

1. 1.« Pourquoi traiter le signal avec des dispositifs numériques ? »
   

C’est une excellente question lorsqu’on se lance dans l’utilisation d’un DSP. Traiter un signal numériquement ne permettra généralement pas de gagner en qualité lorsque, par exemple, on souhaite filtrer un signal. Le gros avantage réside avant tout dans la flexibilité du système. Ainsi, alors qu’un filtre passe bande analogique aura une fréquence relativement bornée et un ordre fixe, un filtre numérique sera plus adaptatif et plus évolutif. Il s’agit là d’un exemple dont l’exactitude pourrait être discutée mais il est important de comprendre ce point avant même de se lancer dans la conception d’un appareil.

Ainsi, je vous relate une expérience démontrant parfaitement ce point. Un récepteur de satellites polaires possède un système de correction de l’effet doppler dû au déplacement du satellite. Cette correction peut être réalisée avec un DSP. La fréquence intermédiaire à la sortie du premier mélangeur d’un tel récepteur est de 10,7 MHz. On peut alors envisager d’installer un DSP à ce niveau, d’échantillonner le signal, d’appliquer une FFT, de chercher le pic du signal et d’asservir ensuite la fréquence envoyée au mélangeur pour toujours avoir le signal centré sur 10,7 MHz. Cette solution nécessite donc au minimum un DSP qui sera capable de traiter des données à 21,4 MHz. Et ceci sans compter les autres opérations que doit faire le processeur : conversion analogique-numérique, commande du système envoyant la fréquence asservie au mélangeur, calcul de la FFT… Voici donc une charge relativement importante. D’un autre côté, l’utilisation d’une varicap couplée à la sortie BF du récepteur pour faire une PLL asservie par le signal de réception est une solution simple, fonctionnelle et très peu coûteuse. Certains diront aussi que l’utilisation d’un DSP permettra aussi de filtrer le signal BF (tant qu’on y est…) et d’afficher la fréquence reçue. A ceci, on peut rétorquer que le filtre peut être fait analogiquement et que l’affichage de la fréquence reçue peut être faite avec un simple microcontrôleur peu onéreux.

Voici donc un exemple illustrant les quelques questions qu’il faut se poser avant d’utiliser un DSP. La suite de ce document ne traitera pas de ce point qui serait trop long pour espérer donner la marche à suivre. Et ce serait dans la limite des spécificités de chaque application.

Mais on peut parfaitement lister ce qui fait que les DSP sont utilisés…

Le gros point fort des transmissions numériques d'informations est leur robustesse face aux transmissions analogiques. On peut en effet ajouter dans le flux de donnée des codes de détection et corrections d'erreur permettant de statuer sur l'état de la donnée, ce qui est impossible en analogique

2. 2.Les avantages du DSP
   

Après avoir dit un peu de mal de ces bêtes du traitement numérique, nous allons voir ce qui fait leur force.

1. •Leur précision : Effectivement, alors que des composants analogiques ont une précision donnée par le constructeur et s’élevant généralement à quelques pourcents, le DSP aura toute la même précision et il sera possible de reproduire un dispositif à de nombreux exemplaires sans devoir recourir à un quelconque étalonnage.
   

2. •La constance : Si en numérique le signal est toujours traité de la même façon indépendamment du vieillissement, de la température… il n’en est pas du tout de même pour un système analogique. Il y aura donc un équilibre à prendre en compte entre le temps pour calculer ces paramètres en analogique et le temps pour développer le programme du DSP.
   

3. •Algorithme adaptive : C’est bien le plus gros avantage du DSP. Il est possible de choisir exactement l’algorithme de traitement parfaitement adapté au système. Et dans certains cas, ce traitement dépend du signal traité, ce qui est généralement très complexe sinon impossible en analogique. L’algorithme pourra aussi être mis à jour par la suite sans modification matérielle.
   

4. •Programmation simple : Les outils de développement pour DSP sont généralement souples du point de vue du langage de programmation (assembleur, C) mais restent limités à un langage impératif.
   

3. III.L’idée même du DSP
   

Observons avant tout un diagramme représentant une chaîne typique d’un dispositif de traitement du signal.

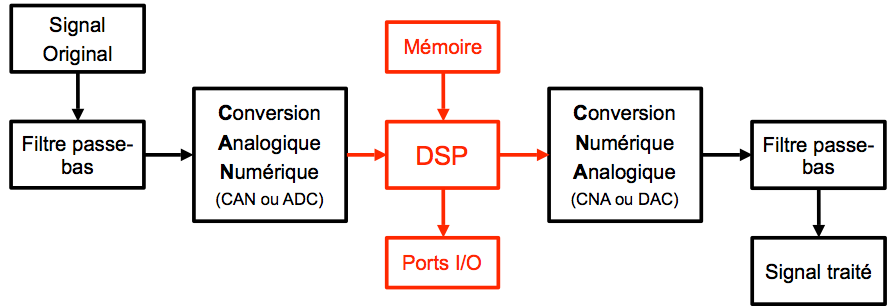
Certains DSP de nouvelle génération intègrent tous ces composants en natif. C’est là que la rapidité devient de première importance. Généralement, les DSP sont prévus pour être installés dans un système autonome et c’est pourquoi ils intègrent presque toujours une RAM pour stocker les données temporaires, une ROM pour stocker par exemple le programme contenant les algorithmes.

On voit donc sur ce diagramme deux composants dont la qualité joue un rôle plus que fondamental : le Convertisseur Analogique Numérique (CAN) et le Convertisseur Numérique Analogique (CNA). Ces éléments influent directement sur la qualité du traitement par leur précision (précision de la référence interne, résolution sur 8, 10, 12, 14 bits ou plus).

Aujourd’hui, les DSP possèdent des fréquences de cadencement allant de 20 MHz à plus de 600 MHz. Il est donc primordial d’avoir une horloge de référence très précise et stable, à l’image des quartz qui sont généralement utilisés. Les DSP les moins performants fonctionnent sur 8 bits mais ils sont vraiment rares. La plus grande partie possèdent une capacité de 16 ou 32 bits.

4. IV.L’architecture
   

Un DSP est avant tout un circuit intégré qui va exécuter des instructions qui auront été définies à l’avance et généralement stockées dans la mémoire programme (EEPROM par exemple).

L’architecture va donc définir les liaisons internes au composant comme la largeur des bus de données, leur nombre et la rapidité de l’unité de calcul.

Chaque bus est aussi relié à un registre temporaire permettant de stocker temporairement les instructions, les adresses, les données. D’autres registres sont aussi présents comme le registre d’état (ou de contrôle) dont les données sont soit en lecture seule soit en écriture seule par mesure de sécurité car ils servent à déterminer précisément le déroulement d’une instruction. D’autres encore permettent de configurer différents paramètres pour les ports (série, DMA…), les interfaces avec des mémoires de sorties, les Timers. Ces derniers ont une adresse en mémoire de données.

Le composant possède aussi une unité centrale, son cœur, dans laquelle s’exécutent les instructions. Ce cœur contient dans la plupart des cas une unique unité arithmétique de traitement des données. Chaque unité de calcul fonctionne sur des registres : un servant à placer les donnés à traiter et dont le contenu est géré par le programme, un autre servant à stocker de façon temporaire les résultats intermédiaires des calculs et un dernier servant au résultat final. Ce dernier est « géré par l’unité de calcul » : ce qui y est stocké sera remplacé lors du calcul suivant.

L’architecture est conçue pour permettrent aux instructions d’effectuer les opérations suivantes en un unique cycle d’horloge :

Prendre les données en mémoire vive pour les placer dans un registre temporaire. Ceci est possible via un bus d’adressage permettant de « cibler » la donnée à extraire de la mémoire et un bus de données qui va délivrer le contenu de la donnée voulue.

Faire le calcul voulu (logique ou arithmétique) sur une ou deux données.

Faire un test sur le résultat (dépassement, signe…).

Faire des modifications sur les registres.

Placer le résultat à l’adresse mémoire prévue.

L’architecture d’un DSP est donc caractérisée par un noyau DSP comportant deux unités de traitement des données contenant elles-mêmes des unités de calcul comme l’ALU (Arithmétic and Logic Unit), le MAC (Multiplier and ACcumulator), le décaleur à barillet (Barrel Shifter) et les multiplexeurs d’aiguillage des données. Un noyau DSP possède aussi un séquenceur qui envoie les adresses des instructions situées dans la mémoire programme et un ou plusieurs pointeurs ou générateur d’adresses qui est relié au bus d’adressage.

Après ces généralités, nous pouvons donc voir que finalement, il existe deux grandes familles d’architecture : l’architecture de Von Neumann et l’architecture de Harvard.

1. 1.Von Neumann
   

Le processeur, via le compteur de programme, sait à tout instant où il se trouve dans le programme et sait donc ce qu’il doit exécuter ensuite. Ceci étant, il faut donc aller chercher les données en mémoire programme avec tout ce que cela implique (adressage, lecture…).

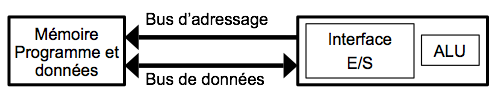
L’architecture de Von Neumann a la particularité de ne posséder qu’une seule mémoire dans laquelle sont stockées instructions et données. Il faut donc partager le bus de données venant de cette mémoire. Cette structure est souvent utilisée pour les microcontrôleurs et microprocesseurs car elle est très simple à manier pour le programmeur. Ainsi, c’est celle qui est utilisée dans la famille des microprocesseurs Motorola 68XXX et Intel 80X86.

2. 2.Harvard
   

Ce nom est très bien porté par cette architecture puisqu’elle a été conçue outre-Atlantique vers 1930 dans l’Université de Harvard.

On voit tout de suite la différence : les mémoires sont séparées. Cette séparation apporte deux avantages majeurs : les adressages et le transit des données sont plus simples et il est possible de placer des données dans la mémoire programme pour les algorithmes complexes.

Cette structure est utilisée pour les microprocesseurs spécialisés et pour des applications en temps réel. C’est donc le cas pour les DSP, hors DSP « low cost », sachant que l’architecture de Harvard est plus coûteuse à réaliser. Cependant, pour réduire les frais de production, certains DSP ont la particularité de ne posséder qu’un seul bus de données et d’adresses à l’extérieur, l’intérieur n’étant pas modifié.

Mais dans la course aux performances, les constructeurs intègrent d’autres technologies comme la méthode du Pipeline.

3. 3.Pipelines
   

Il s’agit plus d’une méthode que d’une spécificité physique. La méthode du pipeline impose une cadence dans l’exécution des instructions en les divisant en quatre opérations élémentaires, optimisant ainsi la rapidité d’exécution générale. Ces quatre opérations élémentaires sont :

1. •Fetch : Extraire l’instruction de la mémoire programme ;
   

2. •Decode : Décoder l’instruction et les adresses des opérandes ;
   

3. •Read : Lire les opérandes en mémoire de données ;
   

4. •Execute : Exécuter l’opération et écrire le résultat.
   

Chacune de ces tâches prend toujours la même durée ce qui autorise leur exécution en parallèle via l’ajout d’un registre temporaire. Voici un tableau illustrant ce système, on y voit clairement l’optimisation.

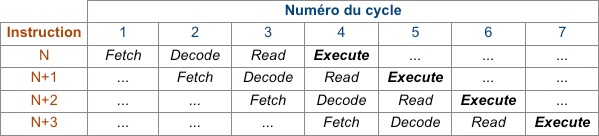
Si une opération élémentaire prend trop de temps, le DSP va décaler les suivantes pour éviter un conflit.

Après avoir vu ceci, il est presque possible de deviner en quoi consiste le prefetch. En réalité, il existe un temps entre l'envoi de l'adresse des données et l'arrivée de celles-ci : le wait state. Pour pallier ce défaut, certaines mémoires utilisent un mécanisme de burst. On affiche une adresse et la mémoire renvoie une quantité variable de données, prises à partir de l'adresse affichée (1 à 8 octets). On gagne donc du temps en mettant en cache ces données directement dans le CPU. L'idéal est d'avoir ce système sur toutes les mémoires (données et programme) mais il est fréquent de ne l'avoir que sur la mémoire programme. Il s'agit donc aussi d'un point très important dans la rapidité d'un système.

Petit exemple : un processeur à N Mhz qui accède une flash de 3 wait states sera aussi rapide à un autre processeur à N/3 MHz et une flash à 0 wait state.

5. V.Les différents DSP
   

Après toutes ces considérations, il reste encore à voir deux points. Le premier est justement une histoire de point britannique qui est en fait la virgule française. Effectivement, certains DSP sont dits « à virgule flottante », en opposition à ceux « à virgule fixe ».

1. 1.A virgule fixe
   

Dans ce cas, les données sont représentées comme des fractions d’entiers qui sont, par exemple, comprises entre -1.0 et 1.0, ou comme des entiers simples. L’avantage de la fraction est de permettre une addition binaire simple des nombres positifs et négatifs (via un complément à 2).

Contrairement aux apparences, un DSP à virgule fixe est plus complexe à programmer qu’un DSP à virgule flottante. Si on prend comme exemple le TMS230C25 de Texas Instrument, les nombres sont codés sur 16 bits mais les calculs sont effectués avec une précision de 32 bits, les 16 bits les moins significatifs étant perdus. Ainsi, le calcul étant sur 32 bits, on évite des erreurs cumulatives. Et même si les registres (32 bits) sont pleins, on peut toujours stocker les données en RAM (16 bits) via deux variables : 16 bits de poids faible + 16 bits de poids fort.

Il faut savoir que certains DSP 16 bits à virgule fixe ne possèdent pas de registre 32 bits. Dans ce cas, la précision est moindre. Et si on doit effectuer un calcul précis, il faudra séparer les parties du calcul en 16 bits et donc effectuer plus de calcul successifs, au détriment du temps. Ce qui nécessite un peu d’astuce et des concepteurs minutieux pour prévoir à l’avance la précision voulue et optimiser les calculs.

Cependant, les DSP à virgule fixe sont plus rapides, c’est donc aussi un critère de choix. Mais avec le temps, les DSP à virgule fixe sont moins développés et on été rattrapés par ceux à virgule flottante dont allons maintenant donner une description.

2. 2.A virgule flottante
   

Ces DSP sont bien plus commodes pour les développeurs. Les données sont représentées avec une mantisse et un exposant selon la formule : n = mantisse*2exposant. On utilise souvent une mantisse fractionnaire comprise entre -1.0 et 1.0. L’exposant indique la place de la virgule en base 2.

Prenons par exemple le TMS320C30 : la mantisse est codée sur 24 bits et l’exposant sur 8 bits, soit 32 bits en mémoire. Lors des calculs, les résultats intermédiaires sont mis en registre avec une mantisse de 32 bits et toujours un exposant sur 8 bits.

Mais le DSP sait aussi manipuler des entiers, donc avec une précision de 32 bits. Ainsi, cette grande plage permet de développer sans vraiment trop se préoccuper de la précision. C’est surtout le prix qui limitera le développement (nombre de broches plus important, surface de silicium du cœur doublée…).

Et pourtant, ils sont très utilisés car plus souples pour des utilisations particulières où :

1. •Les coefficients dépendent du temps (filtre adaptif) ;
   

2. •La structure mémoire est importante (traitement d’images) ;
   

3. •La précision est primordiale, sur un intervalle relativement large.
   

6. VI.La puissance de calcul, notions de base
   

1. 1.Classification rapide
   

Pour déjà avoir un ordre d’idée, le plus lent de tous est le microprocesseur. Il est peut-être lent, mais il n’est pas spécialisé donc polyvalent. Derrière, on trouve les microcontrôleurs, plus rapides mais aussi plus spécialisés. Ensuite les composants logiques classique (PLD plus ou moins inclus selon les technologies) qui sont très rapides et très peu spécialisés. Et environ au même niveau de puissance, les DSP, mais qui sont très spécialisés. On pourra se demander pourquoi on n’utilise pas des composants logiques classiques. Et bien tout simplement car le DSP est spécifique.

2. 2.Une spécificité faisant la force du DSP
   

Ou plutôt, pourquoi le DSP ? En fait, la spécialité du DSP qui le rend si intéressant est sa capacité de calcul. Nous avons vu un peu avant que le noyau du DSP contient plusieurs unités de calcul. C’est juste cela qui le rend performant car il ne lui faut qu’un seul cycle pour effectuer cette opération :

MR = X.Y+R

Afin de donner un ordre d’idée, un processeur classique a besoin d’environ 70 cycles pour faire une multiplication et 10 cycles pour l’addition. Il en sort rapidement qu’un DSP sera très rapide comparé à ses concurrents pour un produit de convolution par exemple.

On comprend aussi pourquoi l’architecture de Harvard est indispensable ainsi qu’au minimum un pointeur.

3. 3.La puissance de calcul d’un DSP
   

Avant tout, voyons les différentes mesures de puissance des processeurs :

1. •MBPS : Mega-Bytes Per Second : permet de mesure la vitesse d’un bus en mégaoctets par seconde.
   

2. •MIPS : Mega Instruction Per Second : Nombre de codes machines (instructions) effectuées par seconde.
   

3. •MOPS : Mega Operations Per Second : Nombre d’opération effectuées par seconde. Par opération, on entend traitement des données, accès DMA, transferts des données, opération E/S,…
   

4. •MFLOPS : Mega Floating-Point Operations Per Second : Nombre d’opérations à virgule flottante (addition, multiplication,…) effectuées par seconde.
   

Le MIPS est préféré pour les DSP à virgule fixe, alors que le MFLOPS est plus représentatif pour un DSP à virgule flottante. Toutefois, une autre mesure existe : le MMACPS noté parfois MMAC ou MMACs. Cette unité signifie Mega MAC Per Second, un MAC étant une opération de base du MAC, le Multiplier and ACcumulator.

A ce stade, il est encore difficile de bien apprécier un résultat de test de rapidité d’un DSP. Il faut savoir que deux DSP à égal MFLOPS peuvent être totalement différents par exemple par leur mode d’adressage. Certains possèdent un système de bits reversing permettant de bien accélérer un calcul de FFT. D’autres paramètres comme le temps d’accès à la mémoire jouent un rôle important dans l’exécution d’un calcul. C’est pourquoi certains DSP intègrent une mémoire locale rapide (comme le cache L1 et L2 de nos processeurs d’ordinateurs). Et enfin, la nature même du code du programme joue un rôle de première importance (surtout lorsque le programme est codé en C et que le compilateur revient à de l’assembleur ou en faire du code machine). Ainsi, un test par benchmark va évaluer un ensemble de paramètres : rapidité du processeur, optimisations matérielles, qualité du compilateur et de la suite de développement,…

7. VII.Test de puissance de calcul
   

Voici un tableau résumant les performances des DSP de la famille ADSP219X produit par Analog Device :

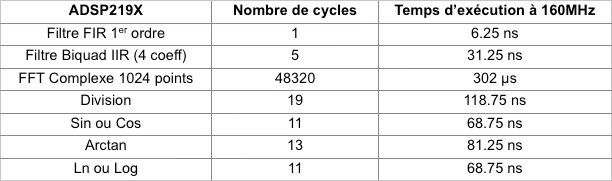
Et un autre tableau comparant différents DSP sur un calcul de FFT 1024 points :

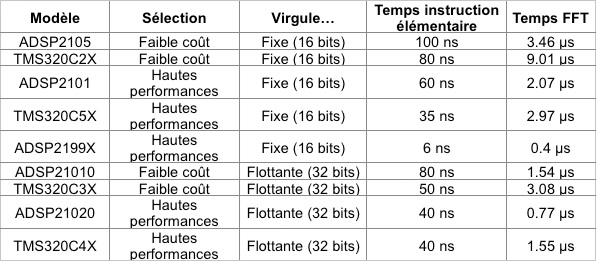
En prenant les derniers DSP disponibles chez Texas Instrument par exemple, on peut nettement voir la différence de puissance entre le meilleur modèle à virgule flottante, le TMS320C6727B-300, et le meilleur modèle à virgule fixe TMS320C6416T.

Même si ces deux DSP font partie de la dernière génération, soit la génération C6000, qui est la plus performante du moment, il y a un net décalage entre les deux. Les données entre parenthèse indiquent les valeurs pour le même DSP, mais avec un modèle conçu pour être cadencé à 600 MHz. On voit tout de suite qu’à fréquence égale, le modèle à virgule fixe est largement plus véloce. Et c’est sans compter sur les technologies embarquées de cette nouvelle génération de DSP  dont voici un bref aperçu :

1. •6 ALU de 40 bits (une fois 32 bits, deux fois 16 ou quatre fois 8 pour chaque) ;
   

2. •Deux multiplieurs de 16 bits ;
   

3. •Registres de 32 à 64 bits ;
   

4. •Deux unités de calcul spécialisées (dont TI vante volontiers les mérites) ;
   

5. •28 opérations par cycle
   

6. •16 Ko de L1P (mémoire cache programme de niveau 1) ;
   

7. •16 Ko de L1D (mémoire cache données de niveau 1) ;
   

8. •1024 Ko de L2 (mémoire cache de niveau 2, utilisable comme RAM) ;
   

9. •Support de SDRAM externe jusque 1280 Mo ;
   

10. •Bus configurable 16/32 bits ;
    

11. •Hôte ou client PCI 3.3V (norme 2.2) ;
    

12. •Et des périphériques habituels comme les ports SPI, etc…
    

8. VIII.Choisir un DSP, les spécificités
   

Le choix d’un DSP est un point qui mérite d’être abordé mais pour lequel il sera difficile de donner un choix « type ». Il faut d’abord correctement cibler l’application voulue. Ensuite, il faut envisager la question de la rapidité minimum requise dans les calculs. Puis évaluer les coûts de développement, en prenant en compte les rapports performances/prix des DSP, les langages de programmation disponibles, etc…

Par exemple, pour une application multimédia et plus particulièrement audio. Il faut un DSP qui aura une grande précision mais sans grande rapidité, la plupart des CNA audio ayant une résolution de 24 bits et travaillant à 192 KHz (en sortie bien entendu). Dans ce cas, un DSP 16 bits ultra rapide à virgule flottante sera un des pires choix faisable (le pire étant un DSP aux même caractéristiques mais lent…). Il faudra donc un DSP pouvant traiter des données sur 24 bits, autrement dit un DSP 32 bits. La virgule flottante est sans intérêt et nuit aux performances. Il manque encore la rapidité du DSP. Pour la déterminer, il faut connaître le type de calcul qu’il faudra exécuter, évaluer ainsi le nombre d’opérations à faire et ensuite rapporter le résultat au fait qu’il faut « rafraîchir » le CNA à 192 KHz. Ainsi on obtient la vitesse minimum du DSP à utiliser.

En revanche, de nombreux DSP sont spécialement conçus et optimisés pour des applications audiovisuelles. C’est aussi un paramètre à prendre en compte : les optimisations spéciales mises au point par les fabricants pouvant accélérer le développement d’une application et l’application elle-même.

9. IX.La programmation d’un DSP
   

Pour programmer un DSP, il faut au grand minimum deux outils : un logiciel générant les données à placer dans la mémoire programme et un programmateur. Le programmateur ne sera pas détaillé ici car spécifique au constructeur du DSP. En revanche, la suite de développement va davantage nous intéresser. Tout d’abord, cette suite est généralement spécifiée pour un langage précis comme le C ou l’assembleur. Dans les deux cas, il s’agit d’un langage impératif, comme le PHP ou l’ASP, dont la particularité est de ne comporter que des opcodes (operation codes) qui sont des instructions élémentaires exécutables par un microprocesseur. On en trouve quatre principales : l’assignation (lecture d’un donnée, calcul et stockage du résultat), le branchement conditionnel (terme transparent comme les suivant), le branchement inconditionnel et le bouclage.

1. 1.En Assembleur
   

Le langage assembleur, appelé plus communément assembleur et abrégé ASM, peut être rapproché du langage machine. Pour un programmeur, c’est la seule façon de créer un programme qui ne sera finalement presque pas modifié lors de l’assemblage, c'est-à-dire lors du processus qui consiste à transformer les instructions sous forme de mots (ou abrégés en anglais) en codes machine à exécuter, en opposition avec l’opération de désassemblage.

Finalement, avec ce langage, il sera plus compliqué d’écrire un programme dans lequel on exécute de nombreux calculs mais il est évident que l’on garde une totale maîtrise de ce que fera le DSP par la suite, dans quel ordre et surtout en combien de cycles.

2. 2.En C
   

Le langage C (qu’il ne faut confondre ni avec C++ ni avec C# qui sont tous deux des langages à objets) est très utilisé pour sa portabilité, sa simplicité, sa performance et sa disponibilité sur de nombreuses plateformes (résultat de plus de 30 années d’existence).

En revanche, il est très souple pour un programmeur non rigoureux qui pourra écrire des programmes impossibles à porter. Il permet aussi de manipuler des pointeurs mémoire qui sont aussi source de bogues.

A la différence de l’assembleur, il faut compiler puis assembler le C dans de nombreux cas. La compilation est un processus qui analyse le code (le lexique, la syntaxe, la conformité aux normes et la structure) puis génère un code en assembleur ou proche de l’assembleur en fonction du compilateur. On procède ensuite à l’assemblage.

3. 3.Comparaison rapide entre assembleur et C
   

Comme déjà dit, l’assembleur permet de garder un contrôle presque parfait du code qui sera mis dans le DSP, contrairement au C où ce code dépend du compilateur. C’est pourquoi les constructeurs mettent à disposition des outils de développement intégrant un compilateur de plus en plus orienté sur l’optimisation du code pour améliorer le temps d’exécution. Mais du code C est environ 30% plus volumineux que l'assembleur, il y a donc un choix à effectuer.

Il faut aussi admettre que le C présente un avantage assez important pour l’utilisation de variables de taille supérieure à la mémoire (64 bits par exemple). Dans ce cas, le programmeur n’a pas besoin d’utiliser plusieurs variables qu’il faut réunir, comme en assembleur. C’est le compilateur qui s’en chargera.

Un autre avantage qu'il ne faudrait en aucun cas oublier, c'est la portabilité du code. Un code C bien organisé est assez facilement portable d'un processeur à un autre (il suffira de modifier par exemple la partie configurant les registres de configuration du processeur ou d'utilisation de certains périphériques comme l'ADC) alors que l'assembleur risque de poser d'énormes difficultés voire même d'être impossible à porter.

Une autre chose qui va jouer un rôle très important est une sorte de précalcul. En effet, si certaines variables ne sont pas modifiées explicitement dans le code (par exemple, si elles sont modifiées dans une interruption), le compilateur pourrait précalculer certains résultats pour optimiser le code. Par exemple, pleins de multiplications classiques en C, avec toujours les mêmes valeurs seront très rapides, même plus qu'avec l'unité MAC. On utilise alors des variables "volatiles", indiquant au compilateur de ne pas rendre constante une opération qui ne l'est pas.

Le C est aussi un beau piège, car les calculs ne passent pas par les unités spécialisées du DSP. Il faut veiller à utiliser des instructions particulières pour chaque addition, multiplication, décalage, etc...

En conclusion, le C est utilisé pour les applications qui n’ont pas trop besoin de rapidité et l’assembleur pour les situations où la vitesse d’exécution doit être parfaitement sous contrôle, mais on peut créer un projet constitué de sources assembleur et C afin de mieux contrôler les opérations critiques tout en gardant une certaine portabilité.

10. X.Applications possibles
    

Voici une liste non exhaustive des appareils utilisant un DSP, ainsi que quelques applications :

1. 1.Domestiques
   

2. •De nombreuses cartes son pour ordinateur ;
   

3. •Les téléphones portables ;
   

4. •Les baladeurs (audio et/ou vidéo) ;
   

5. •Certains lecteurs DVD, décodeurs TNT ;
   

6. •Certains amplificateurs audio ;
   

7. •Certains modems ADSL2+ ;
   

8. •…
   

9. •
   

2. 2.Industrielles
   

3. •Les transmissions radio ;
   

4. •Les filtres numériques (passe-bande, passe bas, etc…) ;
   

5. •Les consoles audionumériques professionnelles ;
   

6. •Les cartes accélératrices de calculs pour ordinateur ;
   

7. •Les oscilloscopes numériques ;
   

8. •Les analyseurs de spectre ;
   

9. •Certains générateurs de signaux (GBF…) ;
   

10. •…
    

11. XI.Se passer d’un DSP ? (FPGA, PLD (SPLD, CPLD, EPLD), PAL, PLA)
    

Certaines applications utilisant des DSP généralistes sont souvent ralenties par ce dernier. L’utilisation d’un circuit logique programmable est alors recommandée lorsque les calculs réalisés ne sont pas trop complexes (pour un filtre par exemple). Ces circuits sont couramment appelés :

1. •PLD : Programable Logic Device (circuit logique programmable) ;
   

2. •EPLD : Electricaly Erasable Programmable Logic Device (circuit logique programmable et effaçable électriquement) ;
   

3. •CPLD : Complex Programmable Logic Device (circuit programmable complexe) ;
   

4. •PAL : Programmable Array Logic (réseau logique programmable) ;
   

5. •PLA : Programmable Logic Array (réseau logique programmable) ;
   

6. •FPGA : Field-Programmable Gate Array (le plus connu, réseau de portes programmabes in-situ) ;
   

7. •...
   

Tous ces composants sont similaires dans leur principe mais diffère par la nature de leurs constituants (RAM, ROM, ou Flash pour la mémoire par exemple).

Certains d’entre eux possèdent même un MAC spécialement implémenté pour le traitement numérique du signal. Leur fonctionnement est facilement imaginable en considérant par exemple le CPLD : il s’agit d’un réseau de portes ET et OU. Le CPLD étant « complexe », il possède aussi une matrice d’interconnexion.

Du moins, pour une utilisation assez peu poussée, ces composants sont assez simples à mettre en œuvre. Si on va plus loin (ce qui est souvent le cas en milieu industriel par exemple), il est très difficile de faire synthèse et routage (même avec des logiciels spécialisés).

Le fait que ces composants soient constitués de logique cablée les rend jusqu'à 75 fois plus rapides qu'un DSP.

Les circuits logiques programmables sont aussi en constante évolution et supportent maintenant les calculs à virgule flottante et la reprogrammation in-situ.

Il ne faut pourtant pas voir là un concurrent au DSP. Ces circuits ne sont pas aussi adaptif qu’un DSP et nécessitent un temps de développement assez important.

Le cout unitaire de ces composants les rends aussi inexploitables sur des produits. Par contre ils permettent de concevoir des ASIC qui peuvent être implémentés pour des productions en série

12. XII.Exemple de carte pour l’initiation aux DSP de la famille DsPIC33 de Microchip.
    

Pourquoi ce composant et pas un autre ?

Tout simplement pour son faible coût, sa polyvalence et la gratuité des outils de développement (sans les optimisations). Ce que je vais vous proposer ici ne fait en aucun cas office de référence et ne vous apprendra pas à programmer. Il s’agit simplement d’une base pour découvrir l’univers des DSP pour un coût faible comparé à la majorité des autres solutions. Il s’agit aussi d’un bon exemple car les DsPIC33 sont des microcontrôleurs intégrant un DSP, soit un outil intégrant plus de fonctionnalités qu’un simple DSP.

Le composant retenu ici est un DsPIC33FJ256MC710, opérant à 40 MIPS. Il est disponible en boîtier TQFP100 au pas de 0,5 mm, utilisera un quartz à 10 MHz (ou 20 MHz sans aucune modification matérielle autre que le quartz lui-même).

Cet ensemble d’évaluation va aussi comporter d’autres composants qui seront généralement placés dans des cartes filles.

Ainsi, j’ai décidé, pour permettre d’échantillonner un signal sans utiliser de ressources du DsPIC, d’ajouter un CAN (ADC en anglais) de performance très acceptable : 250 Millions d’échantillons par seconde. Pour un Processeur à 40 MIPS, c’est plus que suffisant.

Une autre fonction externe a été ajoutée : un synthétiseur numérique direct (DDS) opérant à 1 milliard d’échantillons par seconde (1 GSPS).

Ces deux composants auraient pu être intégrés à la carte mère mais leur niveau de performance et leur polyvalence les rendent intéressants pour d’autres applications. La carte fille correspondante est donc conçue pour permettre une réutilisation aisée du composant.

La carte audio permet d’utiliser le DSP dans son domaine d’application le plus courant. Elle est surtout intéressante pour faire une application concrète, « palpable ».

Le petit plus de la liaison USB permet d’utiliser la carte sur un ordinateur sans trop de contraintes. La liaison USB n’étant rien d’autre qu’une émulation d’un port série sur l’ordinateur. Cette connectique autorisera aussi l’utilisation d’un bootloader. Le bootloader est un microprogramme placé en mémoire du DsPIC qui le rend reprogrammable à souhait sans utiliser de carte de programmation, uniquement via le port USB.

Des ports supplémentaires ont été installés sur la carte mère pour permettre d’ajouter d’autres périphériques.

Voici un diagramme très simplifié de l’ensemble des cartes :

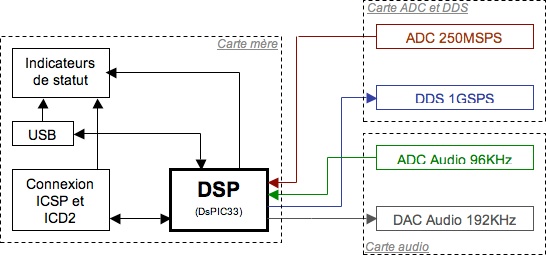
1. 1.Carte mère DsPIC33FJ256MC710
   

Liste des fonctions implantées :

1. •Horloge 6 MHz ;
   

2. •Liaison USB ;
   

3. •Conversion 5V vers 3.3V des signaux série ;
   

4. •Alimentations 5V et 3.3V ;
   

5. •Horloge 10 MHz ;
   

6. •Processeur DSP ;
   

7. •Connecteur de programmation (ICD2 et ICSP) ;
   

8. •DEL d’indications de statut ;
   

9. •Micro-switch en entrée sur le DSP ;
   

10. •Connectique 16 points pour les différentes liaisons ;
    

11. •Connectique 2 points pour l’alimentation 5V.
    

La liaison USB est basée sur le circuit intégré FT232BL fabriqué par FTDI. Ce composant est assez simple à mettre en œuvre. Effectivement, il ne nécessite qu’un quartz à 6 MHz car il dispose d’une PLL intégrée permettant d’atteindre les 48 MHz de l’USB. Le reste ne constitue que les éléments de stabilisation. Ceux qui auront lu son datasheet sauront aussi qu’il permet l’utilisation d’une EEPROM externe pour que le périphérique USB possède son propre identificateur matériel. Le point le plus intéressant pour notre utilisation est qu’il accepte d’avoir son interface de sortie à des niveaux différent du TTL. Il est donc inutile d’ajouter un convertisseur 5 V <=> 3.3 V en sortie.

Ce qui n’est pas le cas des liaisons série qui doivent subir ce changement de niveau. C’est le TXS0104E fabriqué par Texas Instrument qui s’en chargera. Il s’agit un convertisseur 4 bits bidirectionnel, disposant d’une interface tri-state. Autrement dit, il peut être désactivé et dans ce cas, ses bornes sont « vues » comme étant de hautes impédances par les autres composants (on a alors 3 états : haut, bas et Hi-Z).

Le DSP en lui-même ne demande guère de composants à part un quartz (il contient une PLL programmable intégrée) et un condensateur de type tantale pour stabiliser le régulateur interne qui alimente le cœur.

Le micro-switch n’est autre qu’un interrupteur miniature, qui est disponible dans une version montable en surface (CMS, ou SMC en anglais). Il est présent pour permettre une plus grande flexibilité dans la programmation du DSP (on peut ainsi prévoir un programme qui active des options sans avoir à reprogrammer le DSP).

La liaison ICD2 et ICSP sont les deux liaisons les plus courantes et les plus utilisées par les développeurs sur PIC. Ce sont des standards. Notons toutefois qu’il est impossible de s’en passer, au moins pour la toute première programmation si on utilise un bootloader et qu’il sera de grande utilité si on souhaite faire un déboguage du programme in-situ.

Dans le répertoire « Fichiers Annexes » se trouvent les documents sources de la platine dans sa version la plus récente. Ainsi, la carte mère est détaillée avec son schéma de principe. La carte d’alimentation est incluse dans la carte mère dans le projet final, cette partie n’étant séparée du reste que par manque de place.
Sont également disponibles les fichiers gerber et drill (les fichiers GBL, GTL et TXT).

2. 2.Carte fille ADC 250 MSPS et DDS 1GSPS
   

Liste des fonctions implantées :

1. •Horloge 250 MHz ;
   

2. •ADC 250 MSPS ;
   

3. •Horloge 2 GHz ;
   

4. •DDS 1 GSPS
   

Cette carte est encore en développement pour le moment, son intérêt étant principalement de pouvoir essayer les composants utilisés dont le constructeur est assez fier. Donc pour le moment, inutile dans le cadre strict de l’utilisation d’un DSP et des mesures de rapidité.

L’horloge à 2 GHz est générée par le circuit *** intégrant une PLL et fabriqué par Analog Device. On pourrait se contenter d’une horloge à 1 GHz, mais la stabilité de la PLL n’étant pas parfaite, il vaut mieux aller plus haut en fréquence et utiliser le diviseur par 2 intégré au DDS.

Ce DDS est le ***, toujours de Analog Device.

Ensuite, l’ADC est le ***, toujours et encore de Analog Device. Il est cadencé à 250 MHz via un diviseur par 8 relié à l’horloge à 2 GHz.

3. 3.Carte fille Audio numérique
   

Listes des fonctions implantées :

1. •Horloge 24,576 MHz
   

2. •ADC 96KHz
   

3. •DAC 192KHz
   

4. •Amplification
   

5. •Connectique 16 points pour les liaisons série
   

6. •Connectique 2 points pour l’alimentation
   

Cette carte est conçue pour se brancher directement sur la carte mère. Elle est aussi en cours de conception.

4. 4.Applications simples
   

L’exemple donné ici va permettre de constater de façon très évidente l’utilité d’une unité DSP, et plus particulièrement le MAC. Nous serons très loin d’avoir abordé la totalité du sujet, des applications et optimisations possibles, mais le résultat sera éloquent.

La carte mère étant équipée d’un port USB, il sera intéressant de l’exploiter pour communiquer via un terminal série. Le code va donc intégrer une sorte de console virtuelle qui interprètera les commandes envoyées. Ce dispositif sera très facilement extensible.

La source est commentée donc assez facile à comprendre. Mais voyons un exemple pour voir les façons de comparer les vitesses : la multiplication.

Définition des variables, à la fois sous forme de fractional et float pour éviter de comparer n’importe quoi. Car la fonction de multiplication utilisant le MAC nécessite des variables de type fractional. Et la multiplication sans MAC (multiplication standard en C avec le signe *) va interpréter les fractional comme des integer (résultat faux pas conséquent). Les float permettent donc d’avoir des valeurs proches des fractional, et on les utilisera de façon à conserver une virgule fixe. Voici la définition d’un panel de valeur (16 de chaque, nous verrons plus loin pourquoi).

fractional a1 = Q15(-0.8);

fractional a2 = Q15(-0.7);

fractional a3 = Q15(-0.6);

fractional a4 = Q15(-0.5);

fractional a5 = Q15(-0.4);

fractional a6 = Q15(-0.3);

fractional a7 = Q15(-0.2);

fractional a8 = Q15(-0.1);

fractional a9 = Q15(0.1);

fractional a10 = Q15(0.2);

fractional a11 = Q15(0.3);

fractional a12 = Q15(0.4);

fractional a13 = Q15(0.5);

fractional a14 = Q15(0.6);

fractional a15 = Q15(0.7);

fractional a16 = Q15(0.8);

float c1 = -0.8;

float c2 = -0.7;

float c3 = -0.6;

float c4 = -0.5;

float c5 = -0.4;

float c6 = -0.3;

float c7 = -0.2;

float c8 = -0.1;

float c9 = 0.1;

float c10 = 0.2;

float c11 = 0.3;

float c12 = 0.4;

float c13 = 0.5;

float c14 = 0.6;

float c15 = 0.7;

float c16 = 0.8;

Q15(); est une macro incluse dans C30 permettant de définir facilement un fractional à partir de sa forme décimale.

On définit ensuite 4 tableaux. Le premier recevra les variables précédemment définies pour ensuite pouvoir y accéder facilement (par l’indice de la case du tableau). Le second et le troisième servent à placer les valeurs source pour les calculs, 256 valeurs car 16*16=256. Le dernier sert à accueillir les résultats.

fractional temp[16];

fractional table[256];

fractional table1[256];

fractional table2[256];

float ftemp[16];

float ftable[256];

float ftable1[256];

float ftable2[256];

On remplit alors les tableaux temporaires :

temp[0] = a1;

temp[1] = a2;

temp[2] = a3;

(…)

temp[13] = a14;

temp[14] = a15;

temp[15] = a16;

ftemp[0] = c1;

ftemp[1] = c2;

(…)

ftemp[14] = c15;

ftemp[15] = c16;

On crée un algorithme pour remplir les tableaux source de telle façon à ce que chaque calcul soit différent si on multiplie les tableaux terme à terme. On évalue ainsi correctement les capacités du processeur et les capacités à utiliser le prefetch. On comprend alors pourquoi 16 variables et 256 cases dans les tableaux.

for(j=0x0; j<0x10; j++) {// 0x10 = 16

   for(k=0x0; k<0x10; k++) {

      table1[j*0x10 + k] = temp[j];

      table2[j*0x10 + k] = temp[k];

   }

}

for(j=0x0; j<0x10; j++) {

   for(k=0x0; k<0x10; k++) {

      ftable1[j*0x10 + k] = ftemp[j];

      ftable2[j*0x10 + k] = ftemp[k];

   }

}

Les données source sont donc prêtes.

Première multiplication et évaluation à partir du compilateur.

VectorMultiply(1,table,table1,table2);        // avec MAC

ftable[0] = ftable1[0] * ftable2[0];  // sans MAC

On a une unique multiplication. En plaçant astucieusement des Nop(); avec des points d’arrêt, on peut facilement évaluer le nombre d’opérations processeur nécessaires pour chaque calcul en utilisant le simulateur et la fenêtre StopWatch de MPLAB.

Résultats : 22 cycles pour l’opération avec MAC contre 121 sans MAC.

Deuxième multiplication, avec les 256 valeurs.

VectorMultiply(256,table,table1,table2);// avec MAC

for(j=0x0; j<0x100; j++){     // sans MAC

      ftable[j] = ftable1[j] * ftable2[j];           // 0x100 = 256

   }

Essayons de prévoir un peu le nombre de cycles :

Dans le premier cas, on aurait bêtement 256*22 = 5 632 cycles.

Dans le second : 256*121 = 30 976 cycles.

Dans la réalité (StopWatch à l’appui), le résultat est plus marqué : 1 042 opérations contre 38 822. Ceci s’explique par le fait que les boucles sont optimisées pour traiter un gros volume de données : elles coûtent beaucoup en nombre d’instructions pour être mises en place  mais ensuite chaque tour de boucle coûte moins d'instructions que sur une architecture RISC.

Au final, on a un écart très important si on se limite à du code simpliste. On peut évidemment optimiser la boucle du second calcul, mais l’écart reste toujours présent (on pourrait diviser par 10 l’écart en optimisant vraiment au maximum et en mettant la boucle à plat). Cependant, les durées en réel ne sont pas comparables à vue (vous pouvez essayer).

Encore 256 valeurs mais en boucle cette fois.

for (i=0x0; i<0xFFFF; i++){            //OxFFFF = 65535

   VectorMultiply(256,table,table1,table2);

}

for (i=0x0; i<0xFFFF; i++){

   for(j=0x0; j<0x100; j++){

      ftable[j] = ftable1[j] * ftable2[j];

   }

}

On exécute 65 535 fois le calcul précédent pour obtenir des durées suffisantes à une mesure à vue.

En ajoutant l’activation d’un port relié à une led, on peut visualiser les durées et chronométrer. Le résultat est effarant pour qui ne s’y attend pas :

À environ 40 MIPS, on obtient un temps de 1,66 secondes avec MAC contre 1 minute et quelques dixièmes sans MAC, et tout cela pour 16 776 960 multiplications.

1. •Tableau résumé
   

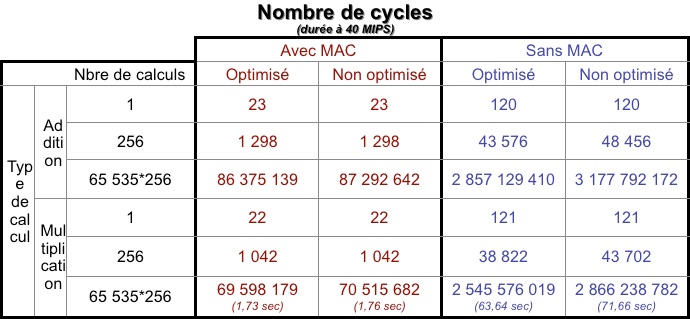
1. •Le meilleur pour la fin : produit de convolution.
   

S’agissant d’une somme de produits, le MAC va pouvoir s’exprimer dans toute son ampleur. On va donc tenter d’optimiser un maximum le code sans MAC pour réduire l’écart.

Microchip propose dans C30 une fonction déjà optimisée VectorConvolve utilisant la DSP Engine.

Voici sa description d’après le manuel :

On a deux vecteurs x et y, de dimensions respectives N et M. On place les coordonnées de ces vecteurs dans un tableau, notons qu’il n’est pas obligé que N=M. On obtient alors deux tableaux tels que :

x[p] représente la pième composante de x qui est de dimension N;

y[p] représente la pième composante de y qui est de dimension M;

Dans tous les cas, M est inférieur ou égal à N (si ce n’est pas le cas, on échange x et y).

Le résultat est r, on associe à r[p] la pième composante de x qui est de dimension Q=M+N-1

La fonction VectorConvolve fait le calcul suivant :

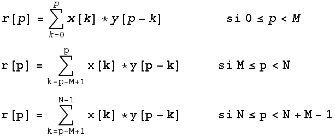
Nous allons utiliser deux vecteurs de 128 composantes, autrement dit, nous allons réutiliser la moitié des tableaux précédemment définis. Cette limitation est due à quantité de mémoire disponible. On pourrait faire les tests séparément mais il faudrait retoucher le code à chaque fois (vous pouvez le faire si vous voulez). Il sera aussi très difficile d’optimiser le code en C (à part une mise à plat des boucles lors de la compilation).

Ainsi, le résultat aura une dimension de 255 (128+128-1).

Le calcul avec l’unité MAC est le suivant :

VectorConvolve(128,128,table,table1,table2);

Et le calcul sans l’unité MAC est calqué sur les 3 formules plus haut. En effet, on pourrait ne faire qu’une seule formule et utiliser des vecteurs de 256 composantes dont les 128 dernières sont nulles... mais on ajoute une grosse quantité de calcul dont l’un des opérandes est nul (voire même les deux opérandes nuls). Vous remarquerez que la deuxième somme n’est plus à faire puisque M = N. Voici donc le code limité au seuls calculs “valables” :

for(p=0x0; p<0x80; p++){

for(k=0x0; k<(p+1); k++) {

ftable[p] = ftable[p] + ftable1[k] * ftable2[p-k];

}

}

for(p=0x80; p<0xFF; p++){

for(k=(p-0x7F); k<0x7F; k++) {

ftable[p] = ftable[p] + ftable1[k] * ftable2[p-k];

}

}

Voici un petit récapitulatif :

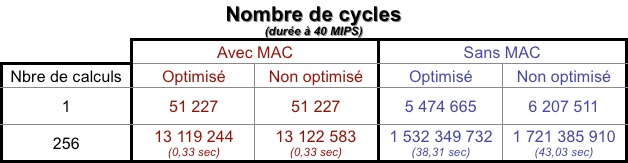
Une fois de plus, le résultat est sans appel, avec un facteur d’écart king-size de l’ordre de 120 !!

5. V.Conclusion
   

Dans ce document, nous avons passé en revue une grande partie des atouts du DSP sans pour autant avoir mis de côté les inconvénients. Il en ressort très nettement ce à quoi il fallait s’attendre : un coeur DSP est extrêmement plus performant qu’un coeur “classique”. Sachez que lors d’un calcul de FFT, le DSP ira environ 100 fois plus vite.

Toutefois, et cette remarque s’adresse particulièrement aux utilisateurs de PIC, ce gain de performance n’est pas valable si l’on reste dans un domaine applicatif où les calculs ne sont pas trop importants.